在复杂系统优化领域，CPLEX整数规划（Integer Programming,IP）凭借其对离散决策变量的精确建模能力，已成为解决资源分配、路径优化、排班调度等问题的核心技术。本文围绕"CPLEX整数规划是什么CPLEX整数规划变量定义与约束条件设置方法"主题，深入解析整数规划的核心概念、变量定义规范及约束构建技巧，并延伸探讨CPLEX混合整数规划分支切割策略，为工程实践提供系统性指导。

　　一、CPLEX整数规划是什么

　　CPLEX整数规划是要求部分或全部决策变量取整数值的数学优化问题，其标准形式可表示为：

　　其中I为需要整数的变量索引集合。根据变量类型差异可分为：

　　纯整数规划（PIP）：所有变量均为整数；

　　混合整数规划（MIP）：同时包含连续变量与整数变量；

　　0-1整数规划：变量取值限制为0或1（如设备启停决策）。

　　CPLEX通过融合分支切割法（Branch-and-Cut）、启发式算法（如Feasibility Pump）和并行计算技术，显著提升大规模整数规划求解效率。其核心优势包括：

　　1.预处理强化：自动检测对称性、聚合约束、固定变量，减少问题规模达30%-70%；

　　2.割平面生成：动态添加Gomory割、覆盖割等强化模型紧密度；

　　3.解决方案池：支持获取多个次优解以应对业务弹性需求。

　　典型应用场景包括：半导体晶圆生产中的缺陷检测路径优化（0-1变量）、物流中心拣货车的装载组合优化（整数变量）、电力系统机组组合调度（混合变量）等。

　　二、CPLEX整数规划变量定义与约束条件设置方法

　　在CPLEX中实现高效整数规划建模，需精准定义变量类型并合理构建约束体系。以下以PythonAPI为例分步说明：

　　1.变量定义规范

　　通过`integer_var`、`binary_var`方法声明整型变量：

　　2.约束条件构建技巧

　　逻辑约束：使用指示约束（IndicatorConstraint）链接离散变量与连续变量：

　　计数约束：通过`sum()`函数处理集合中满足条件的变量数量：

　　分段线性约束：使用`piecewise`函数处理非线性成本结构：

　　3.模型验证与调试

　　启用`parameter.mip.display=4`输出详细求解日志，通过`conflict_refiner`定位不可行约束：

　　三、CPLEX混合整数规划分支切割策略

　　“CPLEX混合整数规划分支切割策略”，针对复杂MIP问题提供高级优化方法：

　　1.自定义分支规则

　　通过回调函数`BranchCallback`实现定制化分支策略：

　　2.动态割平面管理

　　Clique割：检测变量间的互斥关系（如两设备不能同时运行）：

　　FlowCover割：增强网络流模型中的容量约束：

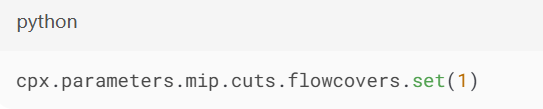
　　3.并行求解加速

　　配置分布式树搜索（DistributedMIP）以利用多机计算资源：

　　案例演示：某电商仓储中心通过以下策略将求解时间从8小时压缩至45分钟：

　　设置`mip.limits.cutpasses=5`增加割生成轮次；

　　启用`mip.strategy.variableselect=3`（强分支策略）；

　　使用`solution.pool`获取Top10近似解供业务部门选择。

　　CPLEX整数规划通过严格的变量类型定义与智能约束管理机制，为解决现实世界中的离散优化难题提供了工业化级工具链。掌握分支切割策略与参数调优技巧，能够在芯片设计、交通网络规划、金融投资组合优化等领域实现决策效率的阶跃式提升。随着CPLEX22.1版本引入量子启发的混合整数求解器，其在超大规模组合优化问题中的表现将更加卓越。