在运筹学和优化领域，CPLEX（IBM ILOG CPLEX Optimizer）是一款广泛应用于解决线性规划（LP）、整数线性规划（ILP）、混合整数线性规划（MILP）等优化问题的强大工具。然而，许多实际问题往往具有非线性的特征，需要通过线性化和参数化的方法将其转化为CPLEX能够处理的线性模型。本文将详细介绍CPLEX模型线性化和CPLEX模型参数化的概念、方法及其在实际应用中的操作步骤，帮助研究人员和工程师高效利用CPLEX进行优化建模。

一、CPLEX模型线性化

1.1 线性化的必要性

CPLEX主要用于求解线性和整数线性优化问题。当面对非线性优化问题时，直接求解可能不可行或计算复杂度过高。因此，将非线性模型转化为线性模型（即线性化）成为求解问题的关键步骤。线性化不仅能够利用CPLEX的高效算法，还能确保求解过程的稳定性和可扩展性。

1.2 线性化的方法

线性化方法主要包括以下几种：

a. 替代变量法

通过引入新的决策变量，将非线性项替换为线性关系。例如，考虑乘积项 x⋅y，可以引入一个新的变量 zzz，并添加约束：

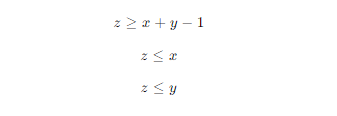
b. 分段线性逼近

将非线性函数在某一区间内用多个线性段近似表示。这种方法适用于函数曲线较为平滑的情况，通过增加线性段的数量，可以提高逼近的精度。

c. 绝对值函数的线性化

绝对值函数 ∣x∣|x|∣x∣ 可以通过以下线性约束表示：

其中，zzz 为新的决策变量，表示∣x∣。

d. 二次项的线性化

对于二次项 x2x^2x2，可以通过替代变量和约束条件进行线性化。例如，引入变量 y=x2y = x^2y=x2，并在特定情况下利用额外信息或近似方法来定义 yyy 与 xxx 之间的关系。

1.3 线性化的实例

假设我们有以下非线性优化问题：

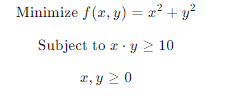
要将其线性化，可以采取以下步骤：

 替代变量法：引入变量 z=x⋅y。

 添加线性约束：由于 z=x⋅y 是非线性的，可以使用分段线性逼近或其他线性化方法对其进行近似。

 目标函数线性化：目标函数中的 x^2和 y^2也需要线性化，可能需要引入新的变量和相应的约束。

由于全面的线性化涉及复杂的数学推导，实际应用中通常依赖专业的优化建模工具或软件库来辅助完成。

二、CPLEX模型参数化

2.1 参数化的概念

参数化是指在优化模型中引入参数，使得模型在不同的参数值下能够灵活适应不同的情境或需求。这在进行敏感性分析、场景分析或多目标优化时尤为重要。通过参数化，用户可以快速调整模型输入，而无需重新编写整个模型。

2.2 参数化的方法

在CPLEX中，参数化可以通过以下几种方式实现：

a. 使用CPLEX参数设置

CPLEX提供了丰富的参数选项，用于控制求解过程的各个方面，如时间限制、节点限制、求解算法选择等。用户可以通过设置这些参数来影响求解过程和结果。

示例（使用Python API）：

python

b. 模型中的可变参数

在模型定义中，使用参数化变量，使得模型的某些部分能够根据参数值动态调整。例如，目标函数系数、约束右端项等。

示例（使用CPLEX的数学编程语言 AMPL）：

ampl

通过改变参数 aaa 和 bbb，可以快速调整目标函数。

c. 使用脚本或外部工具

通过编写脚本或使用外部工具（如Excel、数据库），动态生成或修改CPLEX模型文件，实现在不同参数下的模型切换和求解。

2.3 参数化的实例

假设我们有一个简单的线性规划问题：

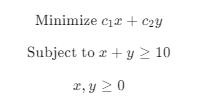
为了参数化系数 c1 和 c2 ，可以使用CPLEX的Python API进行如下设置：

python

通过修改变量 c1 和 c2 的值，可以快速生成不同的优化问题并求解。

三、总结

CPLEX作为一款强大的优化求解器，在处理线性和整数优化问题时表现卓越。然而，许多实际问题具有非线性特征，需要通过线性化方法将其转化为CPLEX能够处理的形式。同时，模型参数化为研究人员提供了灵活调整模型输入和进行敏感性分析的能力。通过掌握CPLEX模型线性化和参数化的技巧，用户能够更高效地构建和求解复杂的优化模型，满足多样化的研究和应用需求。

在实际应用中，建议结合CPLEX的官方文档和相关优化理论，深入理解线性化和参数化的方法，以充分发挥CPLEX在各类优化问题中的强大功能。